기초 이론

서론

모든 생물은, 미미한 미생물로부터 인간과 거대한 고래에 이르기까지 산소에 의존하여 살아가고 있습니다. 동시에 어떤 물질이든 산소가 있으면 산폐하여 질이 떨어지게 됩니다.

즉, 금속은 산화하여 녹이 슬고 의약품과 음식물을 산폐케 합니다.

생명 활동, 광합성 작용, 일상생활에 있어서 산소와는 밀접한 연관성이 있으므로 많은 과학자들이 다양한 환경 조건하에서 산소 농도치를 측정하는 방법을 연구하게 되었습니다.

한편으로 이러한 연구의 목적이 충분한 산소량이 생명체의 건강을 보장한다는 것을 밝히기 위한 것입니다.

다른 한편으로는 산폐하는 물질의 파괴를 막기 위하여 산소를 아주 없게 하거나 저농도의 산소만이 있도록 체크하기 위한 것입니다.

기초 이론

이 장에서는 Orbisphere 계측기의 개발과 사용법에 있어서의 배경이 되는 기초 이론을 다룬다. 우선 산소 농도 측정의 다양한 방법을 연구하면서 우리는 농도를 직접 측정하는 방법을 택하지 않고, 그 대신 측정 매체 내의 산소 활동성, 즉 산소치의 분압을 측정하는 방법을 택하였다.

그러므로 본장의 목적은 서로 다른 측정 매체에서의 산소의 농도와 활동성 사이의 관계를 설명하는데 있다.

     Pi α Ci

우선 우리가 호흡하는 대기를 생각해 보자. 이것은 78%의 질소, 21%의 산소, 1% 아르곤, 그리고 다른 불황성 가스 미소량과 다양한 부유 물질로 구성된다.

다음으로 일정한 체적 V 내에 포함된 기체 혼합물의 총압력 P를 상정해 본다. 우리가 아래 보여준 그림은 공기가 가득찬 풍선을 보여준다. 압력이라 함은 오로지 풍선 안측 표면에 부딪히는 기체 분자에 의해 풍선 내부의 단위 면적에 가해지는 힘을 말한다.

총 압력은 구성 가스의 분압의 합계와 같다는 것이 1801년 DALTON 에 의해 알려졌다.

     P = ∑i Pi

그러므로 하나의 가스의 분압은 일정한 체적 즉 풍선 내부에 그 가스만이 있다고 가정할 때 그 가스가 가하는 압력이다.

     P_O2 = PARTIAL PRESSURE

이제 압력과 가스가 들어 있는 용기의 체적간의 관계를 살펴보자. 분자의 수가 일정할 때 체적이 감소하면 단위 시간에 단위 면적에의 분자 충돌 수는 증가한다. 이것은 BOYLE 에 의해 아래와 같이 표현되었다. (1662년)

일정 온도에서의 가스의 압력은 체적에 반비례한다.

     P α 1 / V

둘째로 입력과 온도의 관계는 거의 1차 함수에 가깝다. 온도가 증가함에 따라 가스 분자의 운동 에너지도 증가하여 단위 시간에 단위 면적에 대한 분자 충돌 율은 증가하게 된다.

따라서 체적이 일정할 때 온도가 높아지면 압력도 높아진다.

이 관계식은 1787년에 CHARLES 에 의해 정립이 되었는데 1802년에 GAY LUSSAC도 별도로 이를 정립하였다. 이를 근거로 추론해 볼 때 압력은 -273.15℃ 에서 0이 될 것이다. 이 관찰 결과에 의해 다음과 같은 절대온도 관계식을 이끌어 낼 수 있다.

     T = t(℃) ＋ 273.15

이와 함께 압력이 일정할 때 가스의 체적도 절대온도 0도 (T=0)에서는 0이 될 것이다.

위 두 가지 원칙을 결합하여 보면 IDEAL GAS LAW 가 아래와 같이 결정된다.

     압력 = (NRT / V),

N: 가스의 mole 상수 (1 mole=6.023 x 10 ²³의 가스분자)
R: 알고 있는 가스 상수로의 비례상수

     p α T / V

     p = NRT / V,

똑같은 법칙이 각각 다른 구성 요소의 가스가 작용하는 분압에도 적용된다.

     P_i = N_i R T / V

N_i = 구성 요소 가스의 Mole 수

주의할 것은 가스 혼합체를 압축시키면 각각의 요소 가스의 분압도 총압력과 같은 비율로 증가한다.

     P_i (압축 후) / P_i (압축 전) = P (압축 후) / P (압축 전)

가스 혼합체의 구성 요소의 농도 C_i 는 IDEAL GAS LAW 에 의하여 그 요소의 분압과 절대 온도로 부터 산출이 가능하다.

     P_iV = N_iRT

     P_i / RT = N_iRT/V

     N_i / V = C_i (단위 체적당 Mole 수)

이 방식으로 가스 혼합체에서의 구성 가스의 농도가 산출 가능하다.

     C_i = (P_i/RT) R은 상수, P_i와 T는 기지의 변수.

이리하여 가스의 분압을 알게 되므로 농도를 도출해 낼 수 있다.

     P_i = NRT_i / V_i

     V / N = C

     P_i α C_i

측정 목적 물질에 따라 가스 상의 산소의 농도나 분압의 어느한 쪽이 더 적합할 것이다. 그러나, 우리가 위에서 고찰한 바와 같이 이 수치들은 다만 가스의 경우에만 해당되는 것이다.

다음은 액체에 적용되는 관계식을 고찰해 보자. 용존 가스 분자가 용기나 액체 내의 다른 침전 물에 부딪치는 충돌 수를 알아내는 것이 이론적으로는 가능하다 할지라도 액체 내의 용존가스의 분압을 논하는 것은 이례적인 일이다. 그 대신 보통은 이러한 충돌을 일으키는 성질을 일컫는 산소의 “Activity (활동성)”, “Fugacity (이산율) 또는 “Tension (팽창성)” 으로 표시하게 된다.

우리는 Fugacity로 표시하기로 하는데 이는 용존가스의 분압에 상당하는 것으로 생각할 수 있을 것이다.

평형상태 (Equilibrium)를 이루고 있는 액체와 가스가 들어 있는 밀폐 용기를 상정해 보자. 평형상태에서는 가스상과 액체상 사이에 모든 구성 가스의 균등한 분배 즉 배분이 이루어진다. 각 구성 가스는 가스상으로 부터 액체내로 용해되어 들어가며 똑같은 비율로 액체에서 가스상으로 증발하게 된다.

이러한 평형상태 하에서는 각 구성 가스의 Fugacity (이산율) 은 가스상과 액체 상에서 똑 같다고 일반적으로 말하여 진다.

가스 상에서의 구성 요소의 분압과 액상에서의 그 구성 요소의 농도 사이의 관계는 1803년에 Henry에 의해 처음으로 연구되었다. 그는 이 수치들 사이의 간단한 1차 비례 관계식을 즉, (Pi=kCi 라는 식) 을 발견하였다.

이 법칙의 현대식 표현은

     f_i = k x_i

f_i = 가스에서의 구성 요소의 FUGACITY (이산율), x_i = 액체에서의 구성 요소의 MOLE 비율, k = 비례상수 (그러나 시스템 내의 온도와 다른 구성 요소의 농도에 영향 있음)

말로 표현하면 Henry의 법칙은 용액 내에 용해되어 있는 가스의 농도는 용액 위의 가스의 분압에 비례한다.

Henry의 법칙의 효용성은 많은 실험에서 얻은 데이터들을 대표되는 것으로 상수 K의 몇 개의 수치의 형태로 간소화할 수 있다는 것이다. 상수 K의 온도에 따른 변화를 나타내는 공식을 알면 더욱 데이터 감축이 가능하다. 그리하면 하나의 간단한 공식으로 어느 순수 용매 내에서 온도나 가스 압력에 관계없이 가스 농도를 계산해 낼 수 있다.

초고압이나 가스와 용매 사이에 화학 반응이 일어나는 상태 하에서는 이 법칙은 통용되지 않는다. 또한 온도의 변화나 용매 내에 녹아 있는 다른 물질의 농도가 변화하면 함수 관계가 성립치 않는다는 것을 꼭 알아두기 바란다.

물에의 산소의 용해 정도는 주로 다음의 세 변수에 영향을 받는다.

     압력 (PRESSURE)

     온도 (TEMPERATURE)

     염분 농도 (CONCENTRATION OF DISSOLVED SALTS)

HENRY 의 법칙에 의하면 용존산소의 농도는 온도와 물 속에 녹아 있는 다른 물질의 농도가 일정하다면 수면에 작용하는 산소의 분압에 비례하여 영향을 받는다.

이것은 곧 분압이 높으면 기체 상태와 액체 상태의 양쪽이 평형 상태에 이르기 전에는 용존 산소 분자의 수도 많다는 것을 말하는 것이다.

일반적으로 가스 용액의 온도가 높아짐에 따라 가스는 용액에서 빠져 나오며 용매의 비등점에서 완전히 없어지게 된다는 것을 잘 알려져 있는 사실이다.

그러므로 총압력이 일정할 때 용존산소의 농도는 온도가 증가함에 따라 제곱 비례 형태로 감소한다.

물의 경우 97℃ 정도에서 용해도가 최소이며 이 범위 이상으로 온도가 증가하는 경우 일정한 가스 압력 하에서 용존 농도가 증가하게 된다.

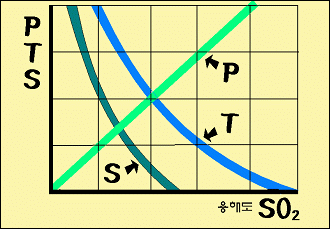
압력과 온도가 일정하면 용해되어 있는 염분의 농도가 증가할 수록 용존 산소 농도는 감소한다.

이는 염분이 추가됨에 따라 용매의 절연 상수의 변화에 기인하는 것이다. 산소는 이온 주변에서 밀려나 물분자에 의해 대치되게 된다. 이것이 염석효과 (SALTING EFFECT) 인 것이다.

이러한 물에의 용존산소의 양을 결정하는 요인들을 도표로 그려 산소의 압력에의 용해 비례성과 온도 상승이나 염도에의 반비례성을 표시하면 다음과 같다.